Optimal Feebas Fishing

08 Nov 2015

TLDR: Just hook one Pokémon per tile. But scroll down for simulation scripts and pretty graphs!

Ah, Milotic. One of my favourite Pokémon in general, but also one of the most rewarding to obtain back when it was first introduced in Gen III. Evolving a Feebas into a Milotic was a unique experience in its own right, but catching that Feebas in the first place was a major challenge.

If you didn’t play any of the original Ruby/Sapphire/Emerald games, or just don’t remember, here’s the deal with Feebas: it can only be found in the wild on Route 119, and only via fishing. And then – and this is what makes it so special – it can only be encountered on six random water tiles out of the entire route - the rest of the tiles only have Carvannah. For reference, this is Route 119:

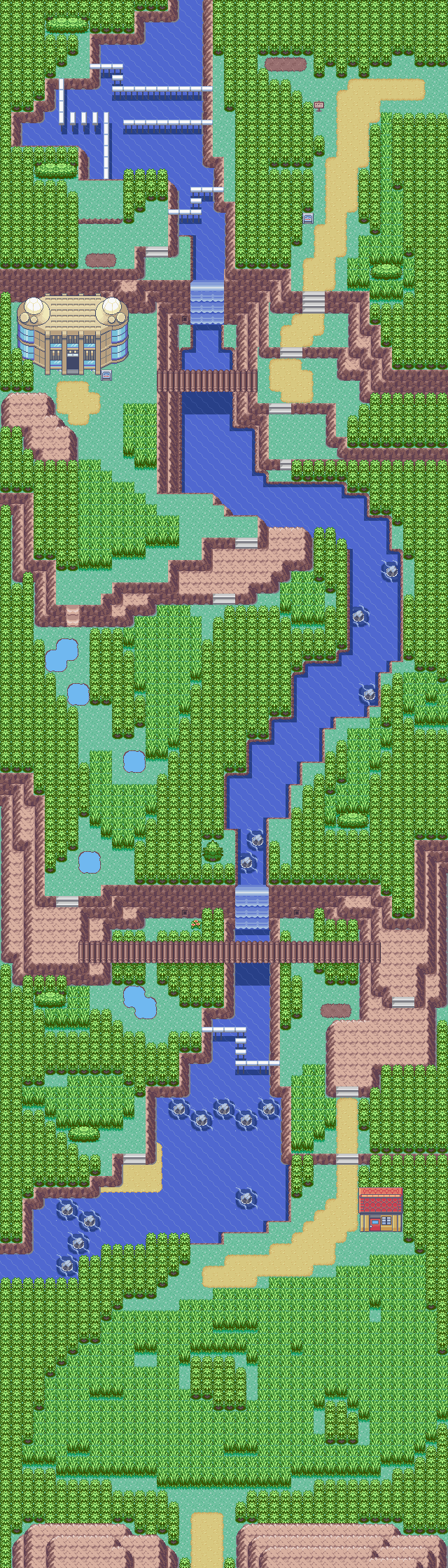
…that’s a lot of water tiles - 446, by my count. At least it’s not Route 124?

Needless to say, in Gen III Feebas is a rare Pokémon indeed. But with a bit of math, we might be able to ease at least some of the pain of finding it. What we know so far:

• N = 446 fish-able water tiles on Route 119
• K = 6 of those contain Feebas

At this point, the optimal (minimal-time) Feebas-finding strategy seems pretty obvious: just systematically cast your line on each accessible water tile, and eventually you’ll encounter our elusive fish friend. This is a classic sampling-without-replacement problem, and so the probability of encountering a specific number of Feebas tiles after checking a specific number of possible Feebas tiles should be given exactly by the hypergeometric distribution.

But… there’s a catch - no pun intended. Even if you’re fishing on one of the six Feebas tiles, you’re not guaranteed to catch a Feebas - you might still get a Carvannah instead! This opens up the possibility of overlooking a Feebas tile by mistake. So, maybe we should fish on each tile more than once. But how many times? We need to balance being sure that our current tile doesn’t have Feebas (cast as many lines as possible) with a desire to find Feebas as quickly as possible (cast as few lines as possible). This is where things get fun! Let’s update what we know:

• N = 446 fish-able water tiles on Route 119
• K = 6 of those contain Feebas
• p = 0.5 probability of encountering a Feebas when hooking a Pokémon on a Feebas tile (according to Bulbapedia)

This one extra p parameter (previously implicitly assumed to equal 1) complicates our math a fair bit. Instead of looking for an analytical solution, let’s do a simulation instead. This is a Julia script that assigns six Feebas tiles randomly, then iterates over all of the tiles, hooking m Pokémon per tile until it finds a Feebas. If it checks all the tiles on the map without finding a Feebas, it starts all over again.

Running the script gives the following output:

Casts per tile | Average total misses | Average total casts
---------------|----------------------|--------------------
      1        |        1.00          |        128.21 
      2        |        0.33          |        169.67 
      3        |        0.14          |        217.96 
      4        |        0.07          |        270.00 
      5        |        0.03          |        326.89 
      6        |        0.02          |        386.64

So it would seem that even though hooking just one Pokémon per tile means accidentally passing over one Feebas tile on average, the speed gains are enough to make it the optimal strategy in terms of minimizing total Pokémon encounters required. For fun, let’s look at the full distributions to see if there are any surprises:

Visualizing the total-hooks-required distributions confirms our conclusion - even though the distribution modes are roughly the same for each option, the higher hooks-per-tile scenarios have significantly fatter tails, pulling up the average encounters required.

So, next time you find yourself in vintage Hoenn fishing for Feebas on Route 119, don’t bother checking each fishing tile more than once. But get comfortable, because you’ll average 128 Carvannah before you find the fish you’re looking for!